Tutoriel
Avant-propos
Ce jeu Mojette est né d'un hasard comme si souvent en recherche. Hasard arrivé après quinze ans de travail sur cette transformée Mojette.
Le but technologique de la transformée Mojette était de générer de la redondance et d'utiliser cette redondance distribuée pour faciliter l'échange de l'information dans des systèmes complexes. Rien de tout cela ici ! Ce site n'a d'autre ambition que de vous amuser en faisant de vous les premiers au monde à tester ce nouveau jeu. J'ai appris à additionner et soustraire avec des Mojettes à mon plus jeune âge. J'espère que ce jeu permettra à des enfants d'en faire autant, et au moins jeunes de conserver ce talent pratique de la vie de tous les jours.
Remerciements
Le premier algorithme et la première mise en oeuvre est de Jeanpierre Guédon. La première mise en oeuvre du site www.mojette.net est de Charles VUKELIC pour son stage de DUT Informatique. La seconde est de Stan KOCKEN et Philippe CAER pour leur projet de R&D ingénieur en Informatique. la version du jeu avec des lettres a été programmée par Antoine NEDELLEC pour son projet de R&D ingénieur en Informatique. C'est Sylvain DAVID, ingénieur R&D chez FIZIANS qui a corrigé tous les bugs depuis le début du jeu. Qu'ils soient tous remerciés içi pour leur contribution.
Jean-Pierre Guédon
Comment jouer ? (1/6)
Règle 1 : Chaque nombre correspond à la somme des chiffres à découvrir dans
chaque case sur la ligne.
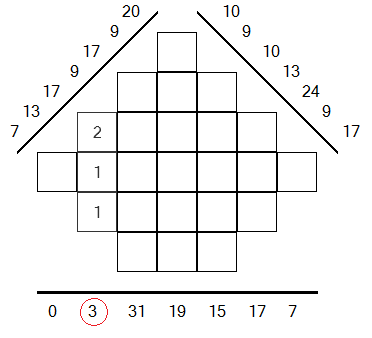
INCORRECT
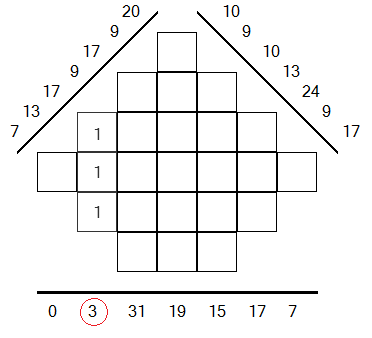
CORRECT
Sur la premère image, la somme verticale 2+1+1 égale 4, ce qui est différent
du résultat attendu pour le bin de la projection du bas (3).
Comment jouer ? (2/6)
Règle 2 : Chaque case de la grille correspond à une valeur d'un chiffre de 0 à 9.
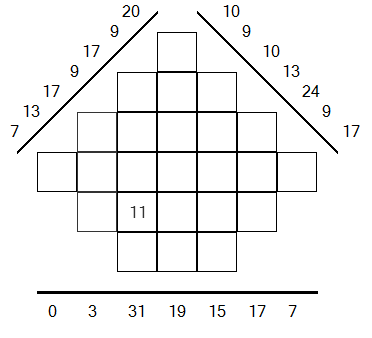
INCORRECT
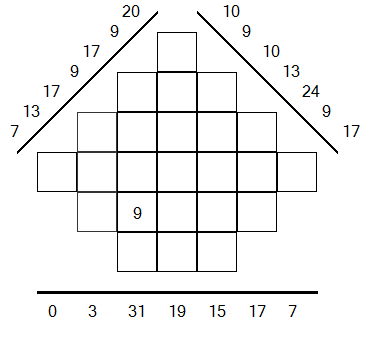
CORRECT
Le joueur a rempli un pixel avec un 11, qui est supérieur à 9 et donc impossible.
Comment jouer ? (3/6)
Règle 3 : Il n'y a que 3 chiffres différents par grille.
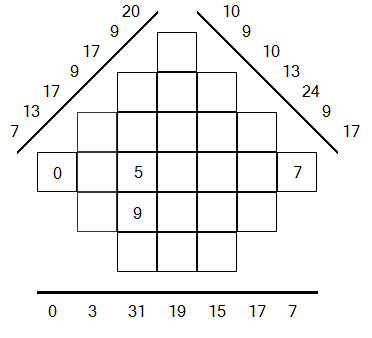
INCORRECT
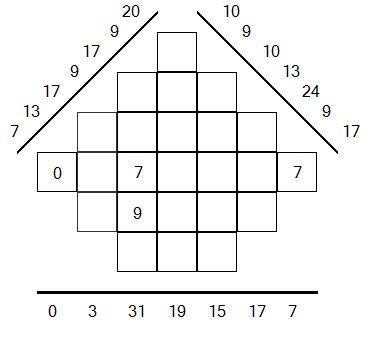
CORRECT
Le joueur a rempli cette grille avec plus de 3 chiffres différents (0,5,7,9).
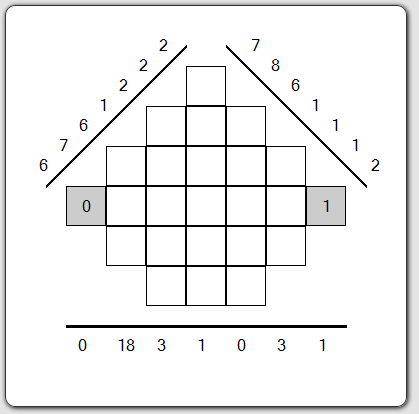
Comment jouer ? (4/6)
Généralement, un ou deux des trois chiffres à découvrir vous sont donnés dans la grille. Cela est explicite sur la forme « diamant 24 » comme dans l'exemple qui suit mais ne l'est pas dans d'autres formes.
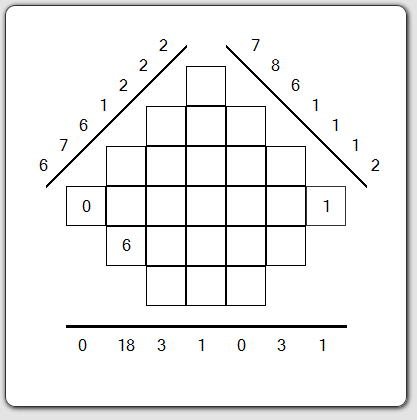
Comment jouer ? (5/6)
La première partie du jeu consiste à trouver ces valeurs. Pour cela, vous devez faire des sommes et des différences pour évaluer sur chaque valeur de projection comment peut se décomposer la somme. Il peut y avoir une somme unique auquel cas on peut parfois commencer à remplir des cases.
Comment jouer ? (6/6)
Il peut y avoir ambiguïté, auquel cas, il faut tenir compte du fait de la règle 3 qui vous impose de ne jamais utiliser plus de trois chiffres différents. L'exemple suivant va vous permettre de mettre en application ces principes.
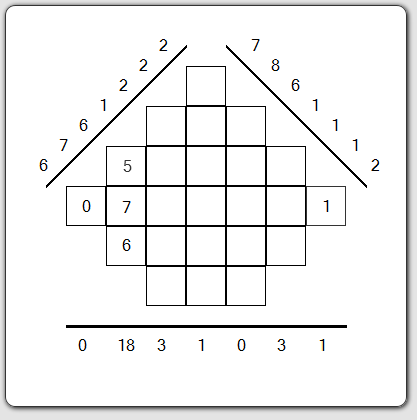
La première grille (1/5)
Voici votre première grille. On distingue donc les trois projections à 45°, 135° et à 90°.
Un point sur un projection est appelé un « bin » comme pour un scanner.
Sur ma projection horizontale, les deux points extrémités sont des bins qui ne correspondent qu'à une seule case, leurs deux valeurs 0 et 1 sont donc déjà remises dans la grille pour vous aider à connaître deux des trois valeurs à chercher.
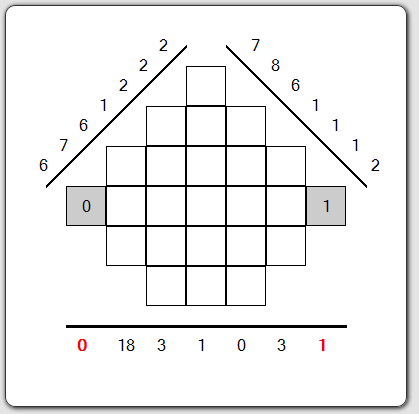
La première grille (2/5)
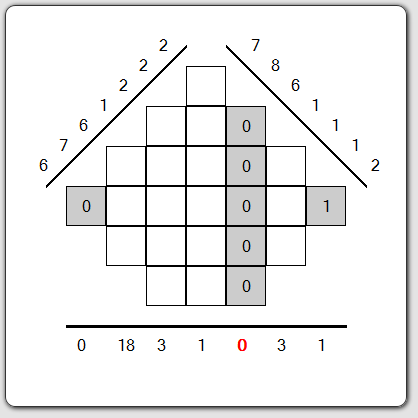
En regardant les différentes valeurs sur les bins, on s'aperçoit du 0 sur la projection horizontale : la seule somme de chiffres qui fait zéro est forcément composée de 0. On les inscrit donc dans la colonne correspondante.
On voit ensuite que le premier bin sur la projection à 45° possède une somme égale à 2 et ne correspond qu'à une seule case non remplie. Par soustraction, on inscrit le 1 dans cette case.
On voit donc que cette première phase du jeu consiste à utiliser les valeurs des bins ainsi que le nombre de cases correspondantes dans la grille.
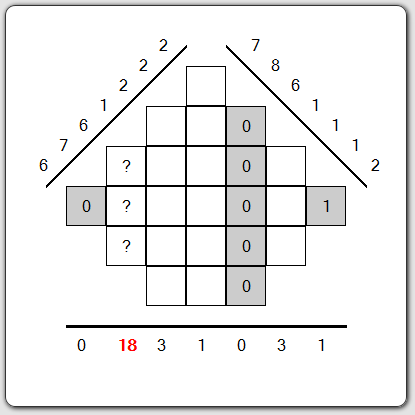
La première grille (3/5)
Ensuite, il nous faut trouver le troisième chiffre. Toujours sur la projection horizontale, on trouve le second bin avec la valeur 18 somme de trois cases. Nous n'avons pas beaucoup de possibilités : soit 18=6+6+6, soit 18=8+8+2 soit 18=9+9+0.
La seconde possibilité n'en est pas une puisqu'il n'y a que trois chiffres au total et que l'on ne peut rajouter à 0 et 1 à la fois le 2 et le 8. Si l'on prend la troisième solution 18=9+9+0, cela veut dire qu'il va falloir au moins 1 bin sur les projections à 45° et 135° avec des valeurs égales ou supérieures à 9 mais il n'en existe pas. Le troisième chiffre à découvrir est donc le 6. Donc on peut remplir les 3 cases de 6 afin d'avoir la somme 18.
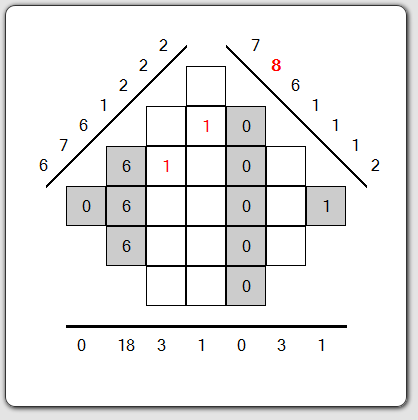
La première grille (4/5)
Après avoir trouvé le troisième chiffre mystère, le reste de la grille se remplit très vite ici (mais ce ne sera pas toujours le cas). En effet, le bin égal à 8 sur la projection à 45° ne peut être obtenu que par la somme 8=6+1+1. On en déduit alors que la colonne de somme égale à 1 doit être complétée par des 0. A vous de terminer la grille !
La première grille (5/5)
Commencez par vous placer sur un pixel, puis remplissez la grille en utilisant le même raisonnement que précédemment. Vous pouvez cocher l'option "soustraction automatique" afin de soustraire la valeur des pixels sur les bins correspondants. Si vous cochez cette option et que vous remplissez correctement la grille, les bins seront donc tous à zéro.
Astuce : vous pouvez vous déplacer plus rapidement dans la grille
en utilisant les flèches directionnelles.
Félicitations ! Vous pouvez maintenant vous mesurer à la
grille du jour
ou découvrir de nouvelles formes en jouant aux
dernières grilles publiées
Précédent
Suivant