Tutoriel | Mojette.net

Foreword

This website is the first one where you can play Mojette. This Mojette Game was born from a chance as so usual with research. The chance did happend after 15 years of hard work onto the theory and applications of Mojette transform.

The technological goal of the Mojette transform was to generate redundancy and to use this distributed redundancy for easily exchange information into complex systems. Nothing like that here ! This website has no other ambition to give you the opportunity to be the first in the world to play with this vous les premiers au monde à tester ce nouveau jeu. I learned doing additions and subtractions with mojettes when I was very young. I hope that the game will allows for kids to do the same, and to olders to keep this practical ability of the all days' life.

Thanks

The first algorithm and implementation have been done by Jeanpierre Guédon. The first www.mojette.net 's version has been done by Charles VUKELIC during his computer science internship. The second version has been developed by Stan Kocken and Philippe CAER for their R&D project as part of their studies in Polytech'Nantes. Version of the game with letters has been developed by Antoine NEDELLEC for his R&D project as part of his studies in Polytech'Nantes. Sylvain DAVID, R&D engineer at FIZIANS has fixed all bugs since the beginning of the game. I thank them all for their contributions.

Jean-Pierre Guedon

How to play ? (1/6)

Rule 1: Each displayed number correspond to the sum of numbers to discover in each location on the line.

FALSE

GOOD

On the first image, you see that the sum of numbers from the second column is different than the bin value(4 instead of 3). Whatever you do thereafter, the grid will be false.

How to play ? (2/6)

Rule 2 : Each grid location corresponds to a single number (from 0 to 9).

FALSE

GOOD

In this grid, the player fulfilled a pixel with a 11 which is not allowed.

How to play ? (3/6)

Rule 3 : There are only 3 different numbers per grid.

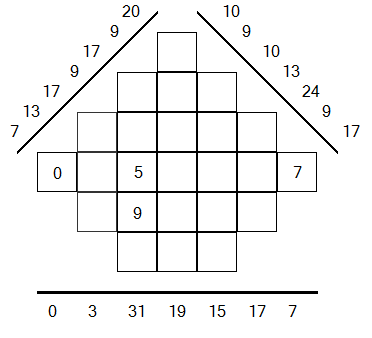
FALSE

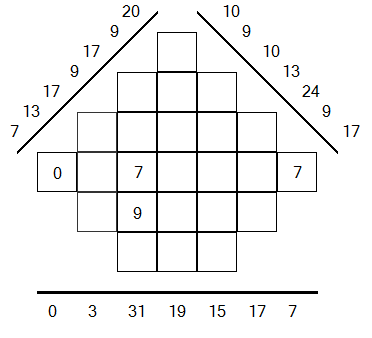
GOOD

The player has fulfilled this grid with more than 3 different numbers (0,5,7,9).

How to play ? (4/6)

Generally, one or two of the three numbers to be discovered are given in the grid. This is pictured on the shape « diamond 24 » as you can see in the next example but can be omitted for other shapes.

How to play ? (5/6)

The first part of the game consists in finding these numbers. For this goal you have to sum and subtract how each value on the projection can be decomposed. Sometimes, there is a unique solution which help you to fill the grid line.

How to play ? (6/6)

There may be ambiguity, in which case it must be borne in mind that rule 3 requires you to never use more than three different numbers. The following example will allow you to implement these principles.

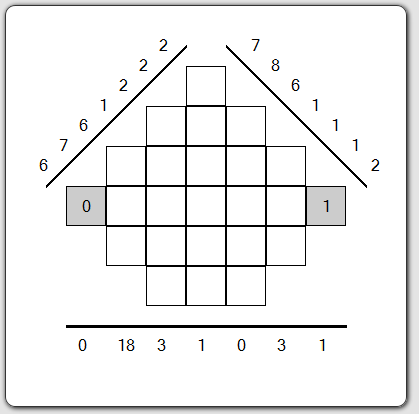
The first grid (1/5)

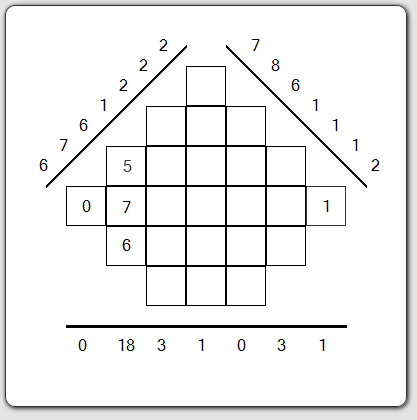
Here's your first grid. We are seeing three projections at 45°, 135° and at 90°.

A point on a projection is called a "bin" as for a scanner.

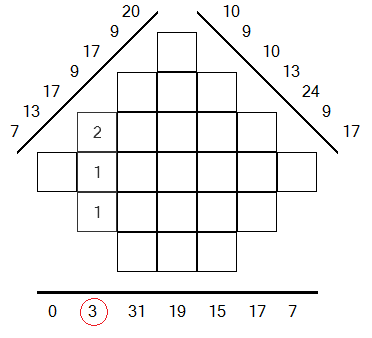
On my horizontal projection, the two end points are bins which are only linked with one box. the two values 0 and 1 are already put into the grid to help you to know two of the three values to search.

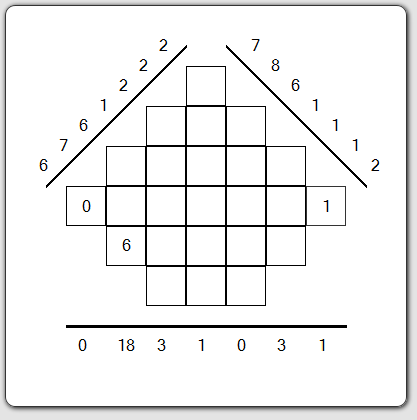
The first grid (2/5)

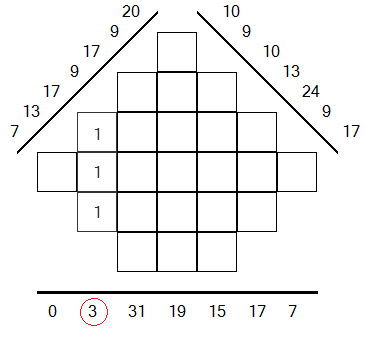
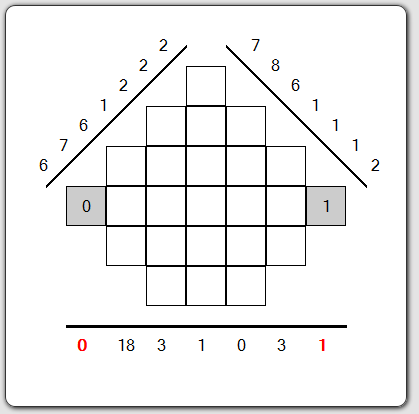
Looking at the different values of the bins, we see the value 0 on the horizontal projection : single sum of the digits is zero is necessarily composed of 0. It shall then be written in the appropriate column.

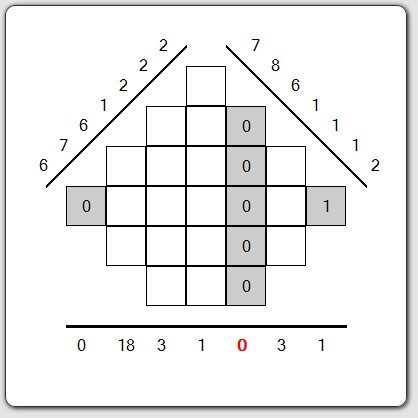
Then, we see that the first bin on the projection at 45° has an amount equal to 2 and corresponds only at one box unfilled. By subtraction, we scored the value 1 in this case.

We thus see that this first phase of game is to use the values of bins and the number of boxes that goes with it.

The first grid (3/5)

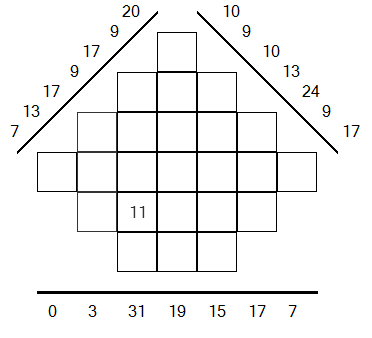
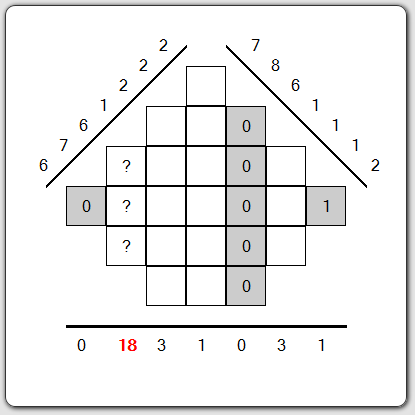
Then we need to find the third value. Always on the horizontal projection, we find the second bin with the value 18 is sum of three boxes. We have not many possibilities: 18=6+6+6 or 18=8+8+2 or 18=0+9+9.

The second option is not possible because there are only three digits in total and we can add the values: 0 and 1 and the values: 2 and 8. If we take the third solution (18=9+9+0), it means that we will have at least one bin on projections at 45° and 135° with value equal or greater than 9 but it's not. Therefore, the third value is 6. So you can fill the 3 boxes with value 6 in order to have the sum of 18.

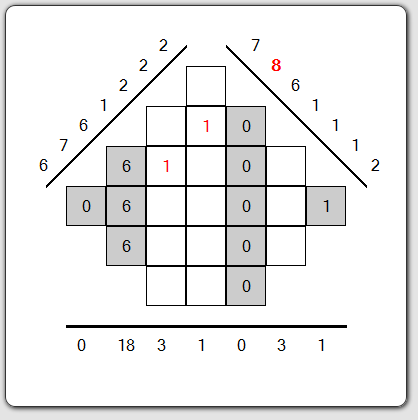
The first grid (4/5)

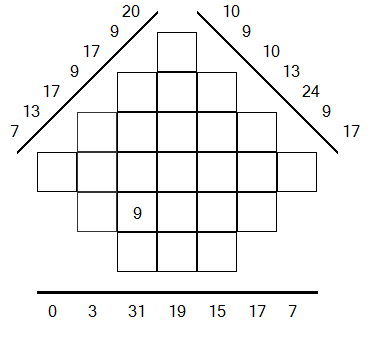
After having found the mystery third value, the rest of the grid fills up very quickly here (but it will not be always the case). Indeed, the bin equal to 8 on the projection of 45° may be obtained by the sum 1+1+6 = 8. Then we can deduce that the column sum equal to 1 shall be supplemented with the value 0. For you to complete the grid!

The first grid (5/5)

Begin by positioning you on a pixel, then fill the grid using the same reasoning as above. You can check the "automatic subtraction" option to substract pixel values in the corresponding bins. If you select this option and that you properly fill the grid, all bins will be at zero.

Tip: You can move faster in the grid using the arrow keys.

Congratulations! You can now play the grid of the day or discovering new forms by playing new grids.